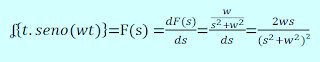3.12 Función Delta Dirac.

http://domisinto.blogspot.com/2011/05/312-funcion-delta-dirac.html

3.11 Transformada de Laplace de una función periódica.

http://domisinto.blogspot.com/2011/05/311-transformada-de-laplace-de-una.html

3.10 TEOREMA DE CONVOLUCIÓN

La propiedad de la convolución  de la transformada la Laplace  relaciona el producto de transformadas y tiene aplicación  en el proceso de inversión  de la  transformada. Suponga que se tiene el producto de las funciones  f(s ) y g(s)  de las cuales se conocen las funciones inversas  f(t ) y  g(t) y se desea encontrar la función inversa del producto  a partir de las funciones inversas conocidas.

Si H(s)  representa el producto de las transformadas y h(t) se la función inversa del producto de la transformadas se puede calcular esta última por medio  de la propiedad de la convolución  de  f(t) y g(t), expresada como: f(t)* g(t), donde el símbolo *  es empleado para la propiedad de convolución .

La propiedad de convolución cumple las siguientes  leyes

a)      Conmutatividad: f(t)*g(t)=g(t)*f(t)

b)      Distributividad : f(t)*¨[g₁(t)+g₂(t)]= f(t)*g₁(t) +f(t)*g₂ (t)

c)      Asociatividad: f(t)*[g(t)*h(t)]=[f(t)*g(t)]*h(t)

3.9 TRANSFORMADA DE INTEGRALES (TEOREMA)

http://ellugardezongua.blogspot.com/2011/05/39-transformada-de-integrales-teorema_17.html

3.8 TRANSFORMADA DE DERIVADAS (TEOREMA).

http://isc-tecnologiaalalcancedetodos.blogspot.com/2011/05/38-transformada-de-derivadas-teorema.html

3.7 TRANSFORMADA DE LAPLACE DE FUNCIONES MULTIPLICADAS POR tn Y DIVIDIDA ENTRE t.

Considérese  la función   f(t) y su transformada de F(s) donde s  es una variable continua. Si se deriva  la función F(s) con respecto a  la variable s de manera consecutiva  se tiene:

De la ecuación 3  se  puede concluir  que al multiplicar por tⁿ  una función  y obtener  su transformada  de Laplace , es equivalente  a diferenciar la función  F(s) n veces y multiplicarla por (-1)^a.

De manera similar, si una función  f(t) satisface las condiciones de existencia de la transformada  de Laplace  y además el 

existe  cuando  t  se aproxima a  cero por el lado  derecho , se cumple que :

Esto  es la integral de la transformada de una  función ʄ(t) equivalente a dividir la función  entre t.

Ejemplo  CÁLCULO DE UNA TRANSFORMADA DE LAPLACE

Empleando la definición  de la diferenciación de la  transformada, encontrar

Aplicando  la diferenciación  de la función  F(s) se tiene

3.6 Propiedades de la transformada de Laplace (linealidad, teoremas de traslación)

http://isc-tecnologiaalalcancedetodos.blogspot.com/2011/05/36-propiedades-de-la-transformada-de.html

3.5.1 TRANSFORMADA DE LAPLACE DE LA FUNCIÒN ESCALÒN UNITARIO

Dos funciones que frecuentemente son usadas en la representación de funciones por tramos son la función escalón unitario  y la función impulso o función  delta. La función  escalón  está definida como:

La transformada de Laplace de la función escalón  calcularse de la siguiente manera

3.5 FUNCIÓN ESCALÓN UNITARIO

Una función que se utiliza muy comúnmente en el estudio de análisis de señales es la función Escalón Unitario o  Heaviside que se define a continuación:

DEFINICIÓN

La función Escalón Unitario o Función de Heaviside se define  como:



Donde a es una constante cualquiera. La gráfica de una función escalón trasladada, por ejemplo con a = 2, es:

La amplitud de la función Heaviside puede modificarse como:

Donde k es una constante cualesquiera. Dependiendo del valor k es la gráfica de la función:

Si k > 0 entonces la gráfica se ve como: (con k = 3).

Si k < 0 entonces la gráfica se ve como:  (con k =  −3)

3.4 TRANSFORMADA DE LAPLACE DE FUNCIONES DEFINIDAS POR TRAMOS.

http://isc-tecnologiaalalcancedetodos.blogspot.com/2011/05/34-transformada-de-laplace-de-funciones.html?zx=b1beec1fa9bb9f5f

3.3 TRANSFORMADA DE LAPLACE DE FUNCIONES BÁSICAS

La transformada de Laplace   se calcula algunas transformadas de funciones básicas  empleando la definición integral de la transformadora de Laplace, en el apéndice 1  se enlistan algunas  transformas  de funciones comunes.

EJEMPLO 1

 Encuentra la transformadora  de Laplace de f(t)=K , donde K es una  constante.

Solución:

EJEMPLO 2:

Encuentre  la transformada  de Laplace de f(t)= t para   t >0.

EJEMPLO 3

Encuentre  la transformada  de Laplace de f(t)= t² para   t >0.

EJEMPLO 4

Encuentre  la transformada  de Laplace de f(t)= t³ para   t >0.

EJEMPLO 5

Encuentre  la transformada  de Laplace de f(t)= tⁿ para   t >0  Y   n  un número entero.

EJEMPLO 6

Encuentre  la transformada  de Laplace de f(t)= t^at para   t >0 ,  donde  a es una constante  .

 EL  SIGUIENTE  VIDEO  NOS  MUESTRA ALGUNOS EJEMPLOS

3.2 CONDICIONES SUFICIENTES DE EXISTENCIA PARA LA TRANSFORMADA DE LAPLACE

Si  las siguientes condiciones   son  satisfechas:

1.-|f (t)|< Mt^a-1en  el intervalo 0≤ t ≤ t₀  donde  M, a y t₀  son algún número positivo.

2.- f (t) es una función  exponencial de orden α (cualquier número real) cuando  t →  ∞(esto es |f(t) | < Ne^at  para t > T donde N y T son números positivos),  y

3.- f (t) es una función continua o continua en tramos (que tiene un número finito  de discontinuidades finitas) en cada intervalo t_o ≤  t ≤ T y t_o > 0

Entonces F(s) existe  para todo s >α. Estas últimas restricciones en  S no limita el uso de la transformada  ya que las restricciones  son condiciones suficientes para la existencia de la transformada de Laplace.

A partir de la definición  de la transformada de Laplace como una integral se tiene que si  se cumple  con las condiciones de la existencia, la transformada será única.

3.1 Definición de la transformada de Laplace.

Introducción

 ¿Qué es una transformada?

Dados dos espacios E y E’ con sendas leyes de composición interna T y T’, de manera que conformen dos estructuras (E T)    y (E’T’)  se llama transformada a una aplicación biyectiva f: E →E que establezca un isomorfismo entre las estructuras (E T)    y   (E’T’)

es decir:

 Definición:

Sea F(t) una función de t definida para t > 0. La transformada de Laplace de F(t), denotada por , se define como:

Se dice que la transformada de Laplace de F(t) existe cuando la integral anterior converge para algún valor de s; de otra manera, se dice que no existe.

Dada una funcion de orden exponencial f : [0,∞) → R, definimos su Transformada de Laplace de la siguiente manera:

donde el dominio de la función transformada D c C, usualmente denotada por la letra mayuscula correspondiente F(s), se toma como el dominio natural que permita la convergencia de la integral.